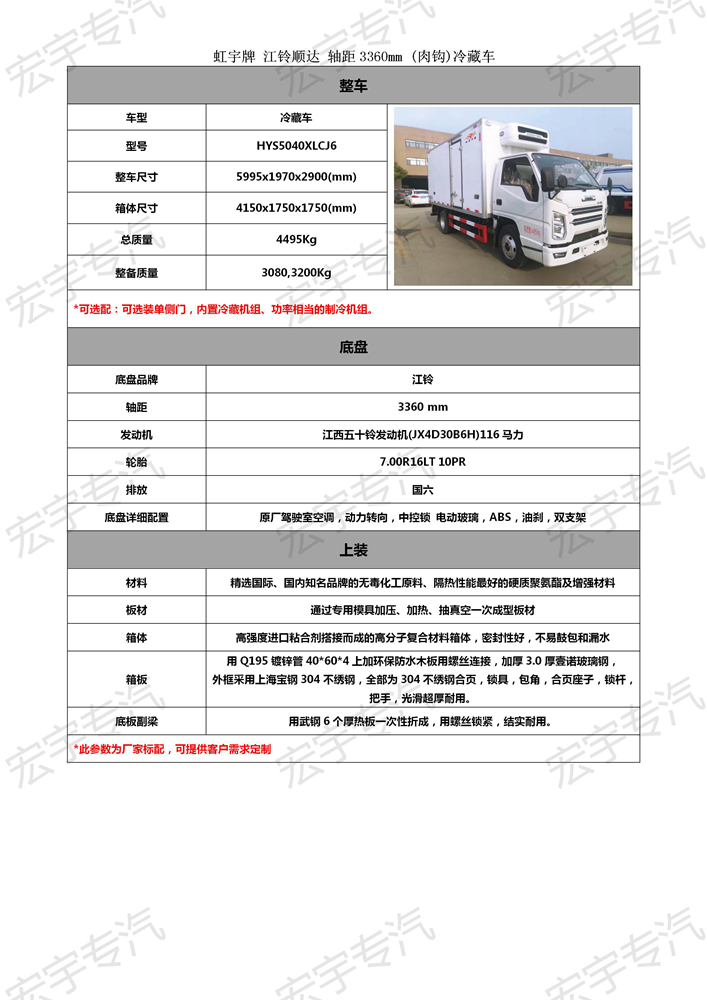
开区间和闭区间怎么用

在数学中，区间是一组由两个数值定义的数集，其中包含了这两个数值以及它们之间的所有数值。在区间中，有两种主要类型：开区间和闭区间。

开区间是指包含了区间两端点之间的所有数值，但不包含这两个端点的区间。开区间通常用圆括号表示，例如(1, 5)，表示1和5之间的所有数值，但不包括1和5本身。

http://www.easiu.com/common/images/1ffPpPG6IP_2.jpg

闭区间则是指包含了区间两端点以及它们之间的所有数值的区间。闭区间通常用方括号表示，例如[1, 5]，表示1和5之间的所有数值，包括1和5本身。

开区间和闭区间在数学中有着广泛的应用，特别是在数学分析和拓扑学中。在这些领域中，区间被用于描述实数轴上的连续性和间隔性。

例如，在微积分中，开区间和闭区间用于定义函数的连续性和极限。在拓扑学中，区间用于定义开集和闭集的概念，这些概念是分析和几何学中很重要的概念。

总之，开区间和闭区间在数学中有着广泛的应用。它们是定义数学概念和定理的重要工具，也是解决数学问题的重要方法。熟练掌握开区间和闭区间的概念，对于学习数学和理解数学概念具有重要的意义。